尚未完成,备份
| 参数(模型大小,静态) | 计算量 | 特征图大小(memory消耗) | 参数自由度(可滑动、复用度) | 特征图的自由度 | 参数的秩/映射能力 | 输出特征图[n,c]的秩/困惑度/表达力 | 评价 | |||
|---|---|---|---|---|---|---|---|---|---|---|
| 全连接 | [$n \times c$, $n \times c$] | $ n \times c \times n \times c$ | 0 | 4 | 2 | |||||
| conv | [k,c,c] | kcn*c | 1 | 3 | 2 | conv局部连接替代全连接+权值共享,大大减少参数,其次减少计算量 | ||||
| conv分解-DSC | [k,c] + [1,c,c] | kc+cc | 2 | 2 | 2 | 对卷积核的rank2分解 | ||||
| conv分解-Flattern | [k] + [c] + [c] | k+c+c | 3 | 1 | 对卷积核的rank1分解 | |||||
| self-attention | ncc3 + nn*d | |||||||||
| RSA | ||||||||||
| 权值共享度越高,参数越少 | 参数秩越高,映射能力越强。 | 减小特征图的秩,类似减少维度、增加正则约束、信息压缩 | ||||||||
| 越少越好 | 越少越好 | 越高越好 | ||||||||
| 这和映射能力是trade off的关系 |
名词
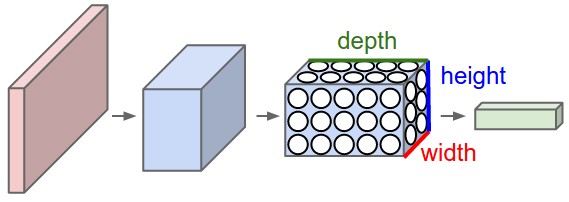
feature map的维度[H,W,C],通常称为[height, weight, channel/depth]
- GConv: group convolution,分组卷积
- 优势: 减少了计算量和参数量,组间独立类似稀疏约束
- 缺陷: 限制了通道之间信息的流动,降低了模型表达能力
- spatial conv,主要
排除法
- **wise: **-by-**的意思,逐个。
- 组词: 一张张,一片片,一个个,一组组,逐点,逐张,逐个,逐组
- 在数学上的概念通常表示单元之间独立。
- PWConv: pointwise convolution, 逐点卷积,[1,1,new_c]
- 也叫position-wise,因为把每次操作一个position,f(position),即position间独立(不交互)。
- 言外之意: 除position以外,其他维度可以交互/不独立,比如
channel combination
- DWConv: depthwise convolution, 逐通道卷积,也叫channelwise,channel by channel的意思
- [w,h,c]
- 每次操作一个channel,以一个channel为操作对象,f(channel),即channel间独立(不交互),不同channel进行相同操作
- 言外之意: 除channel以外,其他维度的交互,比如:
spatial convolutionperformed independently over every channel of an input - depthwise则是极致的group,有多少个channel就分成多少组。讲的真清楚,但是这样做是不是太狠了?channel之间的交互一点都不剩了
- 实例:
- 机器翻译中常用的attention,是position之间的交互,channel之间无交互
- 深度可分离卷积: 将普通的卷积运算拆分成逐通道卷积(depthwise convolution)和逐点卷积(pointwise convolution)两部进行,有效地减少了计算量和参数量;减少了多少?
pointwise group convolution怎么跟depthwise差不多啊?
- 逐点群卷积
汇总
- 全连接,是[W,H,C]整个feature的全连接
- 卷积,是局部feature的全连接。
- 即[w,h,c] 维度上的全连接
- 当$whc$,计算量仍然很大
- 当w=W,h=H 时,也叫全卷积,就等价于全连接。
- 1*1卷积是channel上的全连接
这些实质是
- 利用稀疏连接(sparse connection)的方式来提高卷积的效率。
- 采用group/split的思想来实现稀疏,简单易行
- 一维卷积: 常用于序列模型,自然语言处理领域。
- 二维卷积: 常用于计算机视觉、图像处理领域
- 三维卷积: 常用于医学领域(CT影响),视频处理领域(时间维度)
一维卷积
1 | 输入特征图: [n,c] # channel即embedding |
二维卷积
1 | 输入特征图: [H,W,C] |
| 参数 | 计算量 | 参数的秩 | 特征图的秩 | 评价 | ||
|---|---|---|---|---|---|---|
| 全连接 | whc1wh*c2 | whc1wh*c2 | ||||
| conv | [k,k,c1,c2] | kkc1c2w*h | conv通过权值共享,大大减少参数,其次减少计算量 | |||
| group-conv | ||||||
| DSC | [k,k,c1] + [1,1,c1,c2] | 2 | 对卷积核的rank2分解 | |||
| Flattern-conv | [k,k,c1] + [1,1,c1,c2] | 对卷积核的rank1分解 |
三维卷积
视频
1 | 输入特征图: [T,H,W,C] |
- 计算量少
- 参数量少
- 内存消耗少
- 映射能力强
- 特征表达能力强
这就是我们的需求,但是很多环节是trade off的关系。
merge的方式
group限制了通道之间信息的流动,降低了模型表达能力,
所以group后一般都会再merge一次。即传统的split-transform-merge架构
- concat:
- concat没有不同channel之间的融合,即仍然保持维度上的独立性。所以一般后面会接channel融合的策略,比如1*1卷积
- 实例: alexNet、Transformer、
- 升维 + sum/mean:
- 一般group内的channel数需要还原。因为如果不还原直接add,group比较多的时候信息损失严重
- 实例: mobileNet
- 升维 + weighted-sum:
- 实例: weighted-transformer、
- shuffle: channel shuffle
- 用处: Channel Shuffle for Group Convolutions
- 实例: ShuffleNet
- 其他策略呢?
卷积 VS 全连接
全连接的结构下会引起参数数量的膨胀,容易过拟合且局部最优。
CNN层改全连接为局部连接,这是由于图片的特殊性造成的(图像的一部分的统计特性与其他部分是一样的),通过局部连接和参数共享大范围的减少参数值。可以通过使用多个filter来提取图片的不同特征(多卷积核)。
麻蛋,这是背课文啊。
卷积在深度学习中的应用
Convolutional neural networks therefore constitute a very useful tool for machine learning practitioners. However, learning to use CNNs for the first time is generally an intimidating experience.

CNN为什么work?
- 局部连接代替全连接,& 权值共享
- pooling层,
- 是
发展
- 2012年, 基于深度学习CNN网络的AlexNet在ILSVRC竞赛的ImageNet上大放异彩
- 检测: 2014年Ross Girshick利用CNN成功取代了HOG、DPM等特征提取, ross等人把目标检测分成了三个步骤,首先是对图像提取detection proposal,其实就是图像中一些可能是检测物体的区域,然后使用cnn对这些proposal进行特征提取,最后用svm对这些提取到的特征进行分类,从而完成检测的任务,这是 Two-stage object detectors鼻祖。
简单卷积
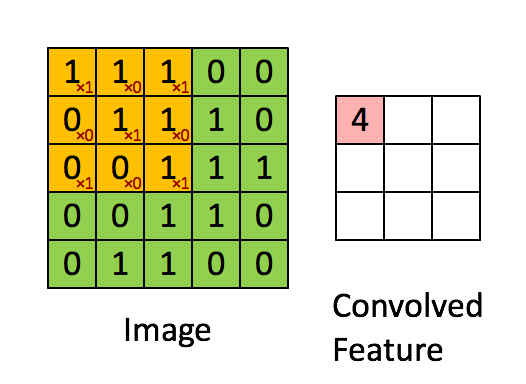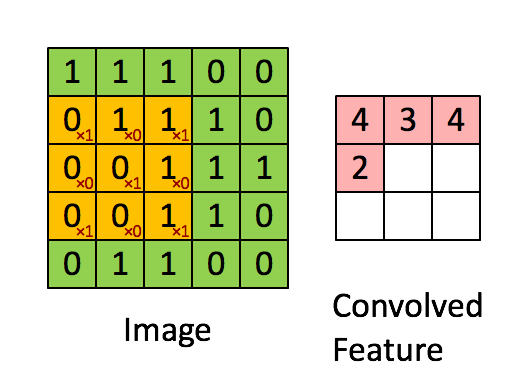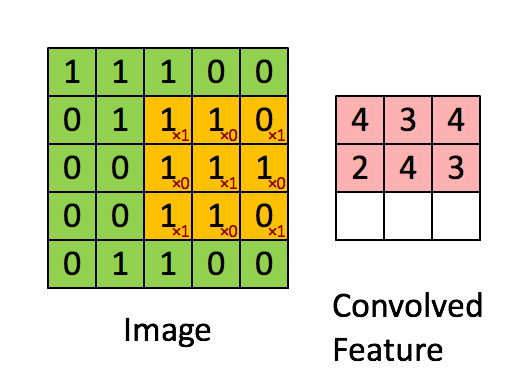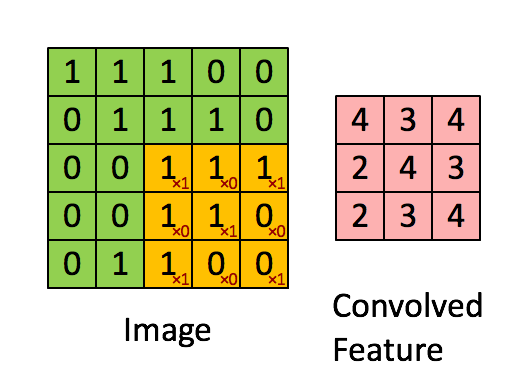
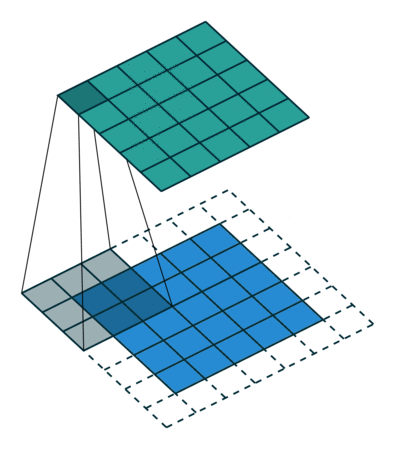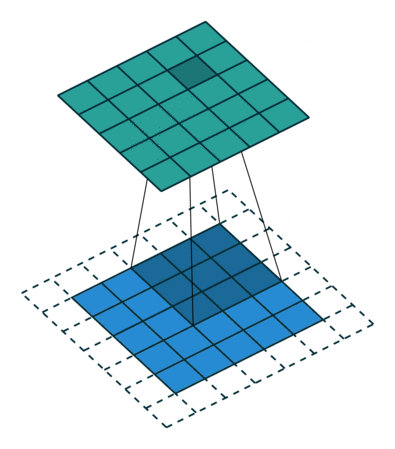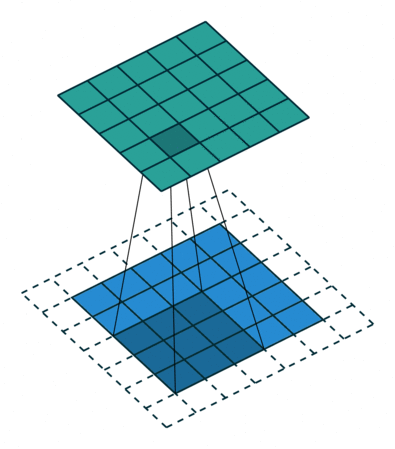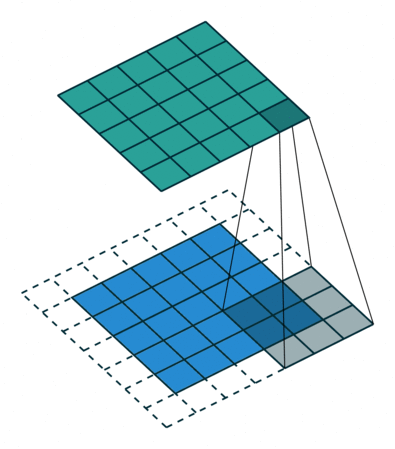
卷积核为3、步幅为1和带有边界扩充的二维卷积结构
- 卷积核大小(Kernel Size):定义了卷积操作的感受野。在二维卷积中,通常设置为3,即卷积核大小为3×3。
- 步幅(Stride):定义了卷积核遍历图像时的步幅大小。其默认值通常设置为1,也可将步幅设置为2后对图像进行下采样,这种方式与最大池化类似。
- 边界扩充(Padding):定义了网络层处理样本边界的方式。当卷积核大于1且不进行边界扩充,输出尺寸将相应缩小;当卷积核以标准方式进行边界扩充,则输出数据的空间尺寸将与输入相等。
- 输入与输出通道(Channels):构建卷积层时需定义输入通道I,并由此确定输出通道O。这样,可算出每个网络层的参数量为I×O×K,其中K为卷积核的参数个数。例,某个网络层有64个大小为3×3的卷积核,则对应K值为 3×3 =9。
卷积的变形
- 关于size
- 1, $1 \times 1$, $1 \times 1 \times 1$
- 全卷积
- 基于分组的
- group conv
- 基于分解的
- 基于
基于拆分/分组的 split/group
group conv
对channel 分group,然后各group独立,最后再合并。
关于group之间是否共享卷积核?以及影响?
实例
AlexNet中采用group conv的初衷是为了利用多GPU。为了减少GPU之间的交互带来的速度影响,只在特定的层才有共享权重
最小 卷积核
最小的卷积核,在1维卷积中是kernel size为1的卷积,二维卷积中是kernel size为1*1的卷积。
这种卷积又被称为Pointwise Convolution,即feature map上的每个point采用相同的卷积操作。
作用
在channel上升维、降维。
$1 \times 1$ 卷积 (二维卷积)
针对[H,W,C]的输入,进行 1,1二维卷积
$$
[H,W,C] \xrightarrow[1 \times 1 \times in \times out]{conv2d} [H’,W’,C’]
$$
1*1卷积并未对图像尺寸进行调整,仅仅是channel之间的融合。
当$out_channel > in_channel$时,起到升维的作用;反之,则起到降维的作用。
1*1kernel广泛用于NIN、GoogLeNet、ResNet
注意
- 缺陷: 1*1卷积并未考虑空间邻域的信息,仅仅是channel之间的整合。所以一般会配合
- 优势: 计算量小,参数少
实战架构:
- 构造bottleneck架构:
- 由于
1*1卷积方便维度变换,很多网络构造bottleneck架构,即高维的IO,低维的middle,目的是在低维下进行复杂运算,减少计算量。 - 注意: 不要为了bottleneck而bottleneck,其根本目的是为了减少计算量。要分析网络的计算瓶颈,再配已适当的策略才是正途。
- 实例: NIN, GoogLeNet, ResNet
- 卷积的分解
- 所有的depthwise seprable convolution
- ss
对应一维卷积,就是kernel_size 为1卷积
最大卷积核 - 全卷积
全卷积(FCN)
1 | 注意区别于FCN架构,见FCN.md |
Transposed Convolutions
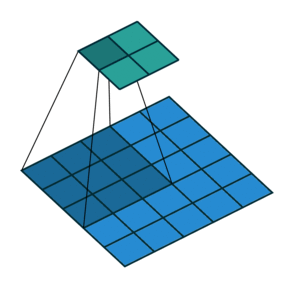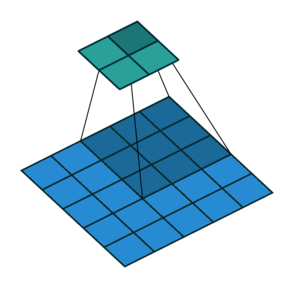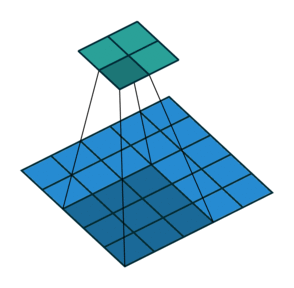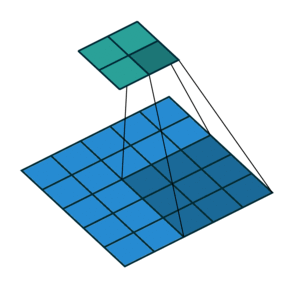
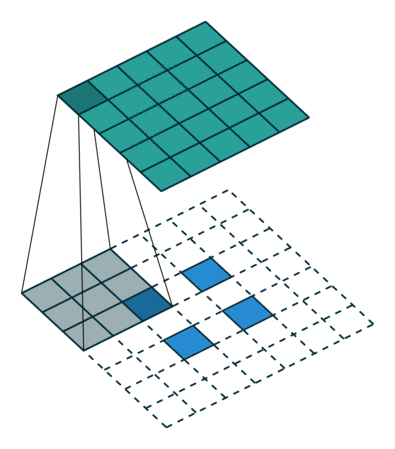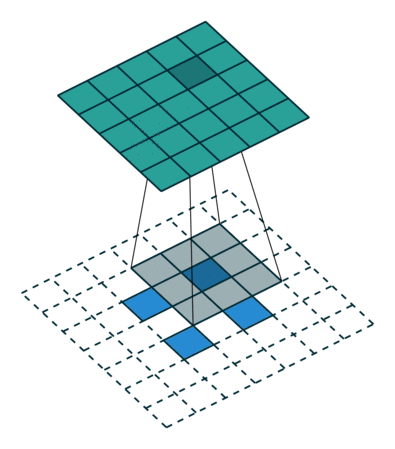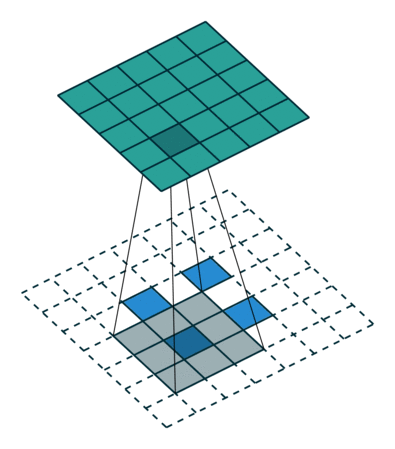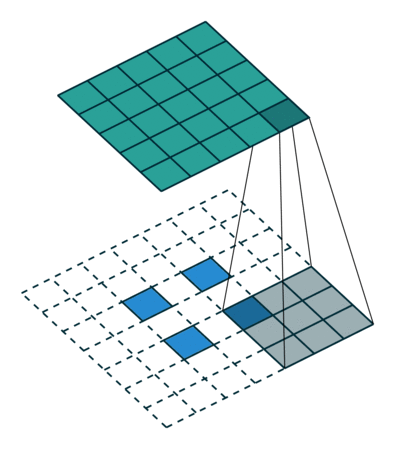
分解
Separable, Factorization
应该是一个意思吧?
- Separable
- 即分离(split)的意思,将传统的一层conv分离为两层,一层用于filtering,一层用于combining
- 不可分离呢?
很自然我们会有两个疑问:为什么要分解?为什么能分解?
为什么能分解?理论基础:
实质是低秩矩阵分解,压缩参数,减少计算量。详见系列3
为什么要分解?优势:
- 加速
- 少参
- 低秩约束
怎么分解?
[n,c_in,c_out]的卷积核
- 满秩分解
- 低秩矩阵分解
- rank=2: 张量乘法分解成两个矩阵乘法
例如: 深度可分离卷积
二维卷积(图像):$[h,w,C,C’] = [h,w,C] * [1 \times 1 \times c \times C’]$ - Rank=1: 即tucker分解,
例如: inception中的某些拆分
- rank=2: 张量乘法分解成两个矩阵乘法
rank=2 深度可分离卷积
深度可分离卷积结构(depthwise separable convolution)
- Depthwise
- depth: channel数
- depthwise: channel之间的操作是独立的,不交互的。
DSC是分解卷积(factorized convolutions)的一种,它将常规的卷积分解为一个depthwise conv与一个1*1 conv。
- depthwise conv: 用于channel内的filtering
- pointwise conv($1 \times 1$): 用于channel间的combining
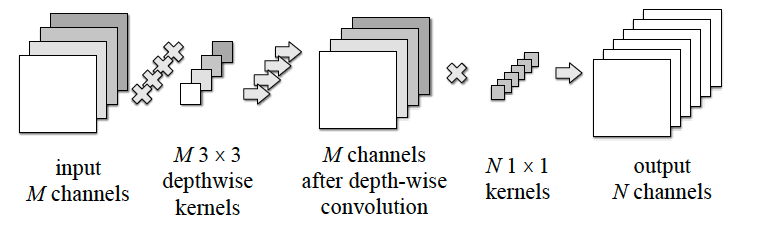
图来源Diagonalwise Refactorization
定义:
DepthSepConv defines kxk depthwise convolution followed by 1x1 convolution
- 因为depthwise卷积是channel间独立的,所以一般会后接1*1卷积,做channel间的融合
传统卷积
$$
[H,W,C] \xrightarrow[k \times k \times C \times C’]{conv2d} [H’,W’,C’]
$$
- 卷积参数量: $k \times k \times C \times C’$
- 计算量:
参数
- depth_multiplier:
- ss
常见误区
- depthwise = conv2d(k,w,C,1)。错误
- depthwise不同于常规的conv2d,是一种的卷积操作,需要经过cudnn加速才能有效果提升。cudnn7.0才开始支持该模块的加速
- depthwise_conv(k,w,C),没有那个1
- depthwise是对所有输入channel采用独立且相同的操作。错误
- 只是独立操作,每个channel的操作不要求相同
为什么depthwise convolution 比 convolution更加耗时? | 知乎
历史 & 应用
- Factorized Convolutional Neural Networks 2016 引用率很低
- Rigid-motion scattering for image classification 2014 首次提出
- Inception models在前几层用到了,用于减小模型复杂度
- MobileNet 2017 首次
- SliceNet 2017 | 机器翻译
factorized convolutions是什么鬼?
- Factorized Networks
- Xception network
- Squeezenet
为什么能降低参数量,同时还能保持精度?
类似矩阵分解的思想。
Group conv是一种channel分组的方式,Depthwise +Pointwise是卷积的方式,只是ShuffleNet里面把两者应用起来了。因此Group conv和Depthwise +Pointwise并不能划等号。
而group卷积只是单纯的通道分组处理,降低复杂度。
rank 1 - Flatterned Convolution
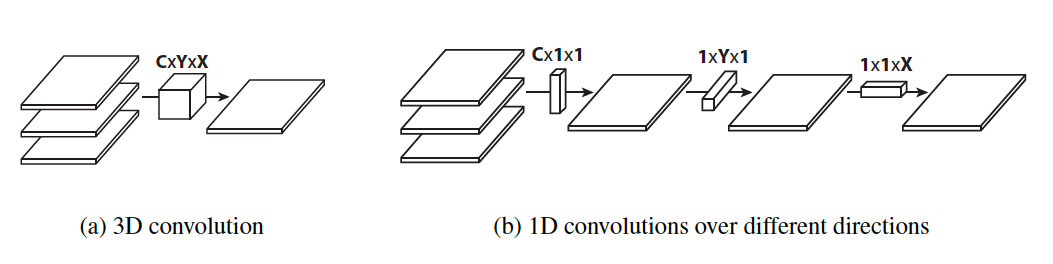
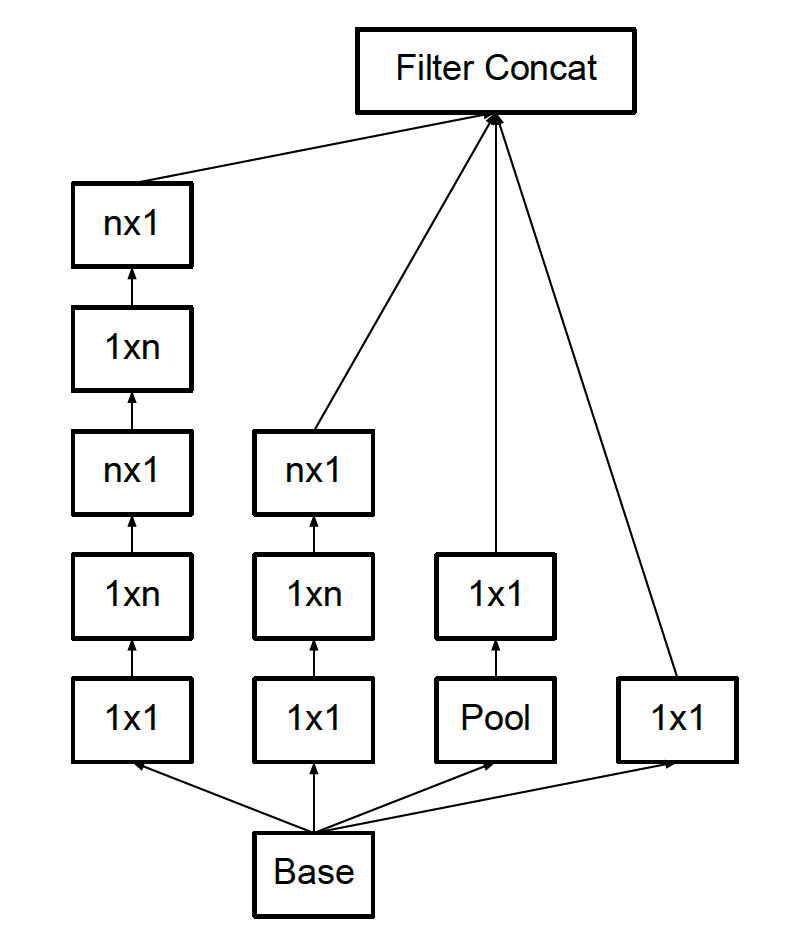
一维卷积
1 | 输入特征图: [n,c] # channel即embedding |
二维卷积
1 |
三维卷积
Dilated Convolutions
空洞卷积(atrous convolutions)又名扩张卷积(dilated convolutions),向卷积层引入了一个称为 “扩张率(dilation rate)”的新参数,该参数定义了卷积核处理数据时各值的间距。
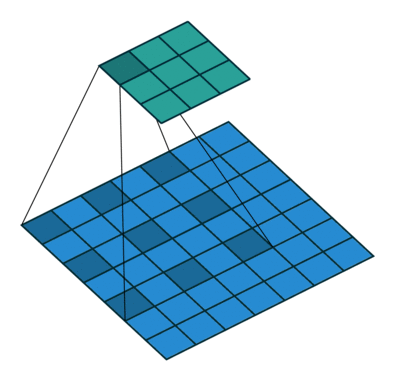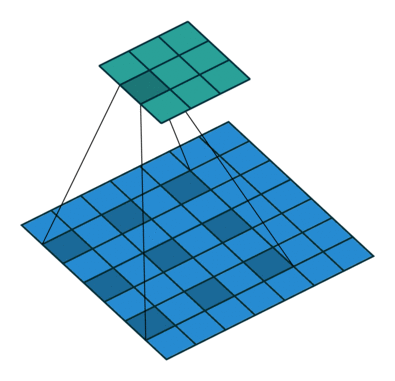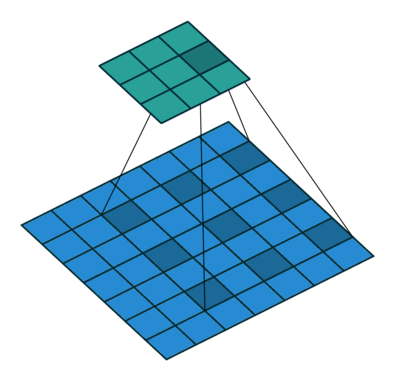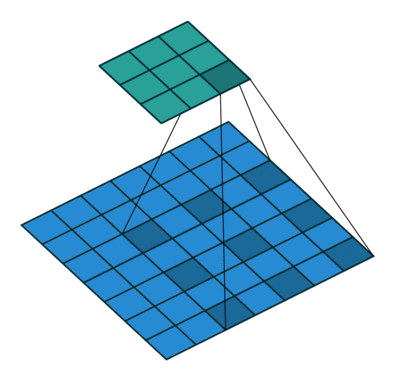
一个扩张率为2的3×3卷积核,感受野与5×5的卷积核相同,而且仅需要9个参数。你可以把它想象成一个5×5的卷积核,每隔一行或一列删除一行或一列。
在相同的计算条件下,空洞卷积提供了更大的感受野。空洞卷积经常用在实时图像分割中。当网络层需要较大的感受野,但计算资源有限而无法提高卷积核数量或大小时,可以考虑空洞卷积。
应用:
- wavenet 音频信号太过密集,比较适合
- SliceNet
Gated Convolution
- Language Modeling with Gated Convolutional Networks
- Free-Form Image Inpainting with Gated Convolution。很牛逼的paper
计算量、复杂度汇总
时间复杂度、空间复杂度
计算量、复杂度的度量,通常用O()来计算。
神经网络也通常用FLOPS来计算。
1 | input: [64,64,3] |
参数共享是一个神奇的东西,参数量剧减,模型小了非常多。
扩展阅读
- Andrew Ng 的UFLDL教程
- 各种卷积结构原理及优劣 | Medium 比较新
- 一文了解各种卷积结构原理及优劣 | Medium & 中文翻译|知乎
- 理解深度学习中的卷积 | Tim Dettmers & 中文翻译 | 码农场
- Understanding Convolutions | colah
- 卷积为什么叫「卷」积? | 知乎
- 如何通俗易懂地解释卷积? | 知乎
- A guide to convolution arithmetic for deep learning