公开密钥密码学
加密需要双方共享一个私密的随机数。从未谋面的两人,如何就此共享密钥达成一致,而又不让第三方监听者知道呢?
离散对数问题
我们需要一种运算,正常容易,反向很难。于是我们找到了模运算,也称时钟运算。
比如 $46 \ \mathrm {mod} \ 12 = 10$,正向计算很容易。
下面采用质数,

对于不同的取值$e$,结果是[0,16]之间均匀分布的。
反向是很困难的
$$3^{\color{red}{29}} \mathrm {mod} \ 17 \xrightarrow[encrypt]{\color{green}{EASY}} {\color{blue}12}$$
正向加密很容易。
求以上过程的反向,这就很难了。
这被称为离散对数问题(discrete logarithm problem)
$$3^{\color{red}?} \mathrm {mod} \ 17 \xleftarrow[decrypt]{\color{red}{HARD}} {\color{blue}{12}}$$
反向解密却很难。已知12,我们只能采用试错法求出匹配的指数。
反向有多难
如果模数很小,比较容易。模数若是长达百位的质数,即便借助地球上最强大的计算机,要遍历所有可能情况也需要上千年时间。
单向函数的强度取决于反向过程所需要的时间。
- 反向的难度,具体计算一下
迪菲·赫尔曼密钥交换
Alice如何向Bob发送信息,而不怕Eve截获信息呢?
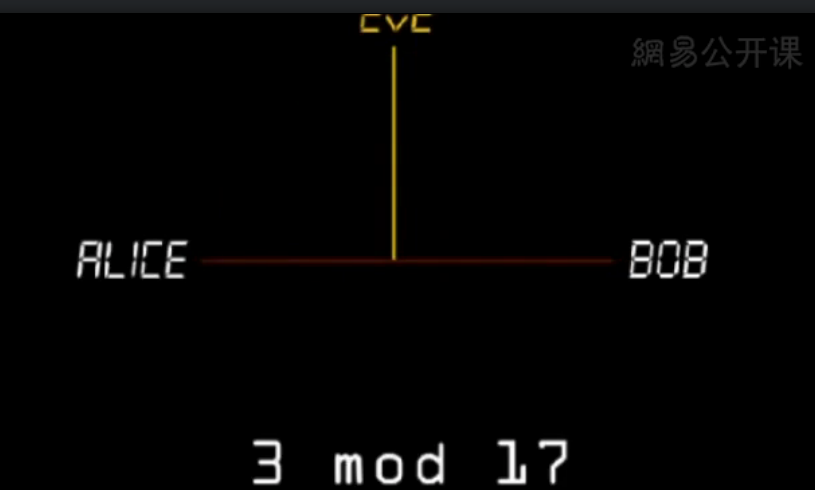
首先Alice和Bob公开地就质模数(prime modulus)和生成元(generator)达成一致,也就是这个例子中的p=17,g=3。
然后Alice选择一个私有数,${\color{red}{15}}$,加密后是${\color{blue} 6}$
$$3^{\color{red}{15}} \mathrm {mod} \ 17 \equiv {\color{blue} 6}$$
然后公开将此结果发送给Bob。
Bob选择一个私有数13,计算
$$3^{\color{red}{13}} \mathrm {mod} \ 17 \equiv {\color{blue} {12}}$$
然后公开将此结果发送给Alice。
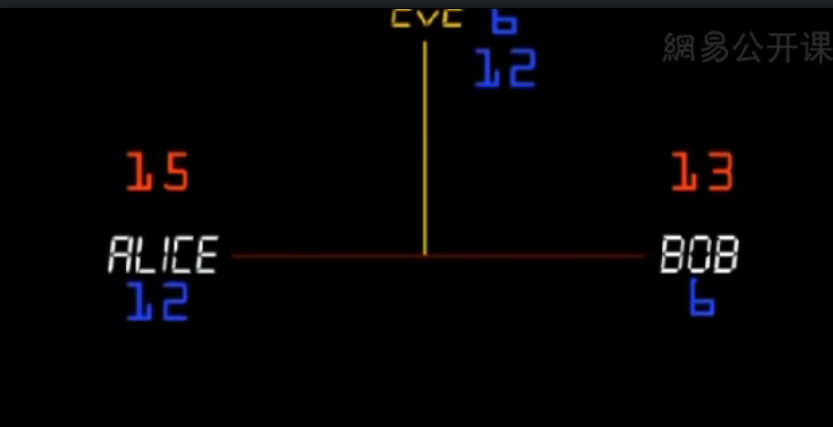
下面就是关键
Alice经过以下计算,得到共享密钥 (shared secret) ${\color{Apricot}{10} }$
$${\color{blue}{12} }^{\color{red}{15} } \mathrm {mod} \ 17 \equiv {\color{Apricot}{10} }$$
Bob也计算得到共享密钥,两者计算结果是相同的。
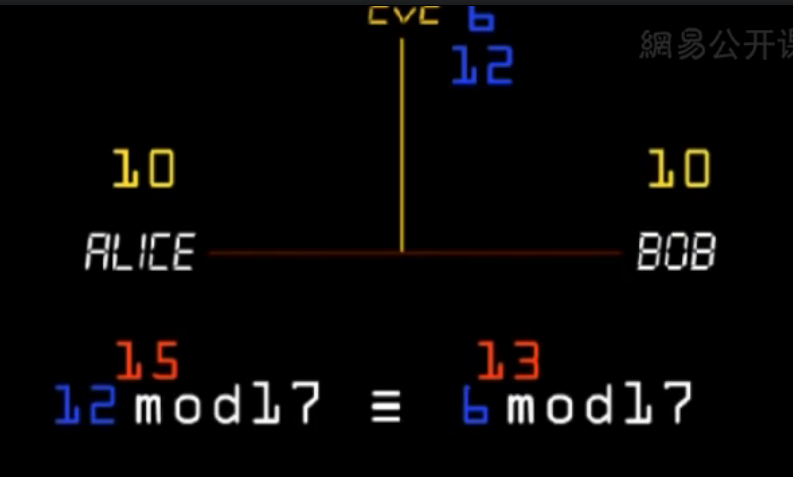
这是因为
$$3^{\color{red}{13 ^{15}} } \mathrm {mod} \ 17 \equiv 3^{\color{red}{15 ^{13}} } \mathrm {mod} \ 17 $$
两种计算实质是相同的,只是指数的顺序不同而已。
没有私有数字 ${\color{red}{15}}$、${\color{red}{13}}$,Eve将无法求出结果。Eve会被困在离散对数问题之中,数字足够大时,实践中,她在合理时限内几乎不可能破解。这就解决了交换密钥的问题。这可以同伪随机数生成器结合使用为未曾谋面的人提供通信加密。
Eve将无法求出结果,没太看懂。
- 这两个私有数字,只要有一个就能解密吗?
- 17,3 是怎么达成一致的?传输过程被截获呢?是public的吗?
RSA加密第一步
对称加密中,要求通信双方共享密钥。但如果Alice和Bob不能实际见面,则需要额外的通信开销,比如使用迪菲-赫尔曼密钥交换。
另外,如果Alice希望同很多人通信,那么她将需要同每个人交换不同密钥。她必须管理好所有这些密钥,发送数以千计的信息,仅仅为了建立它们。
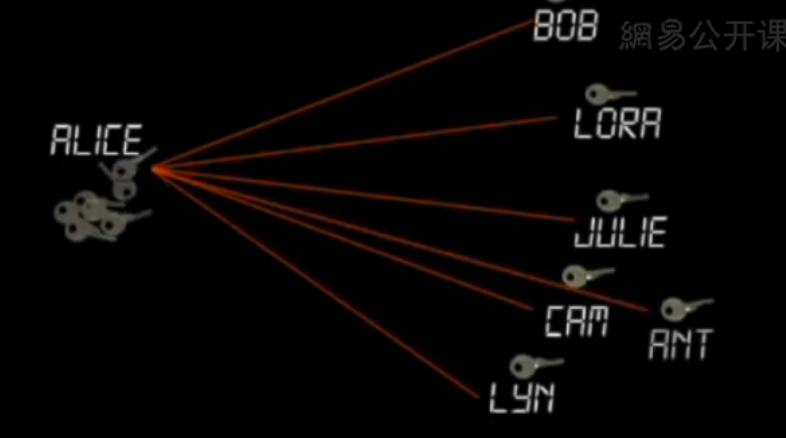
是否有更简单的额方式?
1970年,英国数学家James Ellis试图实现公开密钥加密(non-secret encryption)。
加密和解密是互逆操作,Alice可以买一把锁,把钥匙留在手里,然后把打开的锁发给Bob。Bob可以将自己的信息上锁,然后发回给Alice。这里无需交换密钥。
这意味着锁是可以公开的,可以让世界上任何人使用它来发信息。而现在Alice只需要留一把钥匙。
Ellis并未找到相关的数学方法,但他提出了应该怎样做的思路。关键在于将密钥分为两个部分,一部分是加密密钥,一部分是解密密钥。解密密钥用于解密这一逆操作,而加密是通过加密密钥进行的。
RSA加密第二步
需要构建一种特殊的单向函数,也叫陷门单向函数(trap door one-way functioin)
这种函数,正向很容易,反向很难,除非你有关于trap door的特殊信息。为此,考虑了模幂运算。
扩展阅读
- 现代密码学 | 可汗学院
- http://www.ruanyifeng.com/blog/2013/06/rsa_algorithm_part_one.html